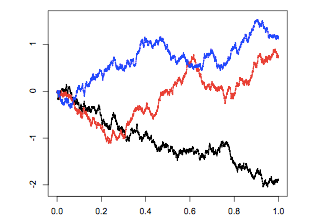
La passeggiata aleatoria, o comunemente “random walk”, è il modello base utilizzato per descrivere i movimenti dei prezzi azionari nei principali modelli di gestione del rischio. È una successione di variabili aleatorie con uguale distribuzione di probabilità e indipendenti l’una dall’altra.
Un esempio elementare di una passeggiata aleatoria semplice è la distribuzione di Bernoulli che assume il valore 1 con probabilità p ( un passo verso destra) e -1 con probabilità 1 – p (un passo verso sinistra) ad ogni passo. La probabilità di andare a destra che a sinistra, vale p=0.5. Se si verificano N realizzazioni, allora abbiamo una distribuzione binomiale
La distribuzione di probabilità è:
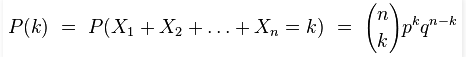
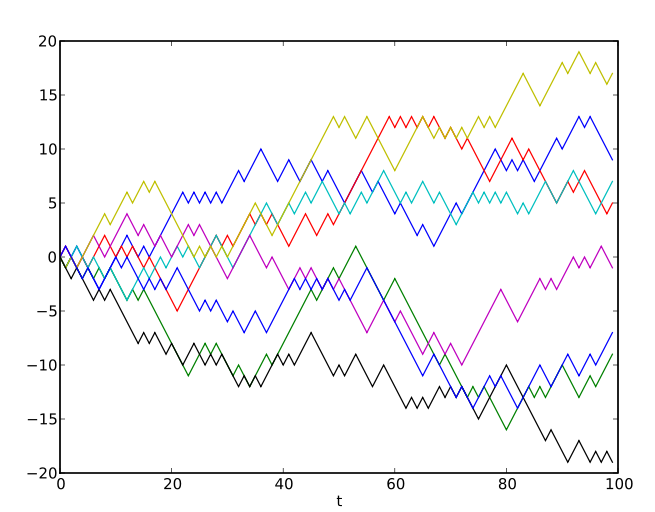
Il moto browniano geometrico è un processo stocastico definito nel continuo in cui il logaritmo della variabile aleatoria nel tempo segue un moto browniano. Tale processo assume particolare rilevanza in ambito finanziario, in particolare nel calcolo del prezzo in quanto nel modello di Black-Scholes-Merton viene ipotizzato che il prezzo dell’azione sottostante segua un tale processo.Il moto browniano geometrico soddisfa la seguente equazione differenziale stocastica:
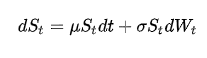
dove Wt è un moto browniano standard, mi il drift percentuale istantaneo e sigma la volatilità percentuale istantanea, sono costanti reali.
L’equazione ha una soluzione analitica nella forma:
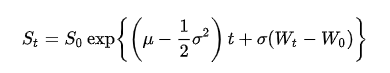
Quando viene applicato ai prezzi, moto browniano presuppone che il passaggio da un periodo all’altro non è dipendente dal livello dei prezzi oppure dalle variazioni dei prezzi. Cioè, ogni variazione è indipendente dalle variazioni di prezzo del passato e la volatilità delle variazioni dei prezzi è costante.